Natural Mathematics Notation and Computer Algebra
Scientific WorkPlace® and Scientific Notebook® are unexcelled in the simplicity of their interface with computer algebra systems. A comparison of the computational features available in Scientific WorkPlace and Scientific Notebook and in traditional computation systems reveals three major differences:
-
When you enter an expression, Scientific WorkPlace and Scientific Notebook derive operations from the natural notation used. For example, if you enter
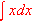 or
or 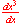 , the program
understands what you are writing and evaluates the expressions appropriately.
This is not possible in other computation systems, because they force
you to be exact with your input syntax. To illustrate this, we enter an
integral using natural mathematical notation) and
press Ctrl+e (or choose
, the program
understands what you are writing and evaluates the expressions appropriately.
This is not possible in other computation systems, because they force
you to be exact with your input syntax. To illustrate this, we enter an
integral using natural mathematical notation) and
press Ctrl+e (or choose Evaluatefrom theComputemenu) to evaluate the integral.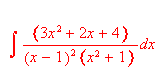
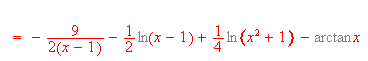
The program automatically places an equal sign between the original expression and the result of the integration. You can use the result of the integration or the original expression itself in subsequent work by selecting the entire expression or some portion thereof. You can perform standard Copy and Paste operations on the expressions as well. You can also save selected math, text, or graphic objects as fragments so that you can recall them for later use.
-
Scientific WorkPlace and Scientific Notebook deduce choices based on familiar notation. In typical symbolic systems, you must use distinct functions to execute the same operation on distinct data types. For example, to factor an integer using one of these other computation systems, you must use the operator
ifactor, but to factor a polynomial, you must use the operatorfactor. In contrast, Scientific WorkPlace and Scientific Notebook examine the object of a particular operation and respond appropriately. To illustrate, you can factor the integer 12345 and the polynomial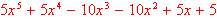 using the same
using the same Computemenu option,Factor.
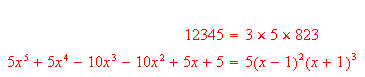
-
With the use of natural interface for both input and output in Scientific WorkPlace and Scientific Notebook, you can select portions of an expression to which you can apply subsequent operations. In contrast, typical computation systems force you to extract and manipulate portions of an expression using special commands. We illustrate this by selecting a portion of an expression to evaluate and having the results replace the selection. This very useful feature is called "computing in place." If you select the rational expression inside the integral
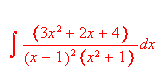
and then hold down the Ctrl key and choose
Partial Fractionsfrom theCompute/Calculussubmenu, this expression becomes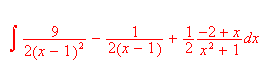
While the expression is still selected, you can click the parentheses icon
 ,
or type Ctrl+9. The expression then becomes
,
or type Ctrl+9. The expression then becomes