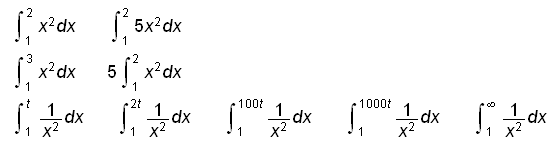Document 101
Making Mathematics Accessible - Scientific WorkPlace, the Syntax-free Electronic Blackboard
Fred Szabo
Professor, Department of Mathematics and Statistics, and Director of Co-operative Education in Mathematics, Statistics and Actuarial Science, Concordia University
Presented April 19, 1996 at the Primer Encuentro Internacional Sobre la Enseñanza y Aplicación de las Matemáticas, ITESM, Mexico.
Today I will explain why and how I have come to use Scientific WorkPlace in my teaching and writing. I will tell you a little bit about Scientific WorkPlace and show you that it is not just another computer program that allows you to do mathematics electronically.
Scientific WorkPlace is the first and only real (perhaps even better than "real") electronic environment for teaching, learning and writing mathematics that allows us to use our standard every-day mathematical notation and does not require computer syntax. With some experience, you will soon find that it will become an indispensable part of your professional tools.
Let us look back in the history of mathematical technology. First there was
-
sand and sticks, then
-
stone and chisel,
-
pencil and paper was a major advance, after that the
-
slide rule, then the
-
calculator, after that the
-
computer with Maple, Mathematica, and other software. But now there is
-
Scientific WorkPlace.
It is now possible to teach interactive courses in linear algebra, calculus, differential equations, etc., that deal dynamically with concepts and calculations through live screen objects that can be manipulated and recomputed instantly ad infinitum.
The arithmetic obstacle to computationally complex problems has been eliminated.
The computational capacity of Scientific WorkPlace 3.5 makes it possible to tackle without trepidation real problems involving, for example, large matrices whose eigenvalues cannot be found algebraically. Such problems used to be relegated to special courses such as numerical linear algebra.
Among the additional features made possible by Scientific WorkPlace 3.5 are the creation of electronic databases in which all definitions, theorems, proofs, and exercises are accessible through the Scientific WorkPlace navigator.
In an interactive session, the database files can be opened as supplementary documents, and the navigator provides direct access to the information in them. Each item can be inspected, copied, and integrated into an active session as desired. This feature provides a new electronic teaching and learning tool.
Since all mathematical data in Scientific WorkPlace 3.5 are live, they can be modified instantly on screen for further analysis and computation. No longer is there any need to erase an example before being able to present a new one or modify an old one. An entire lecture can be relived by scrolling through an evolving document. This permanent record of a teaching session can be placed on a server or copied to a student's diskette and provides a good basis for home study.
As you examine some of the different features of Scientific WorkPlace this afternoon, you will quickly realize that there are at least five basic levels at which you can use this tool to help you in the learning and teaching of mathematics:
-
as a sophisticated scientific editor in which you write out your work or rewrite your lecture notes and assignments, using natural mathematical notation;
-
as an enriched scientific calculator in which you can either carry out individual computations or verify the accuracy of manual computations;
-
as a scientific wizard which can assist you in solving difficult problems if you are concerned with finding an answer to a problem without worrying how the answer is arrived at or how it is mathematically justified;
-
as a scientific explorer which allows you to use the solutions to mathematical problems as new computable objects. You explore their properties by varying some of their data, letting the wizard produce new solutions and then analyzing the mathematical similarities and differences of the obtained solutions;
-
as a scientific stenographer which allows you to abbreviate frequently used material and store it as fragments for future recall.
As you become familiar with Scientific WorkPlace as a scientific explorer, you will value the fact that it allows you to ask what-if questions and provides quick answers. By comparing these answers with your questions, you deepen your understanding of the why of subjects such as linear algebra. If you are unsure of the how , you can always test your understanding by solving problems step-by-step, and then verify your answers with the help of Scientific WorkPlace, the scientific calculator. You can save all of your work electronically for future reference and reuse it, taking advantage of Scientific WorkPlace, the editor. The teaching and learning environment provided by Scientific WorkPlace is therefore much more than an electronic blackboard. It is an environment that integrates the tools required to deal harmoniously with the what, how, and why aspects of mathematics.
Versatility
-
You can use Scientific WorkPlace to do (discover) mathematics.
-
You can use Scientific WorkPlace to learn mathematics.
-
You can use Scientific WorkPlace to teach mathematics.
-
You can use Scientific WorkPlace to apply mathematics to other fields.
-
You can use Scientific WorkPlace to create beautiful mathematical documents.
Our Focus will be on Learning and Teaching
Let me begin by drawing a short comparison between Scientific WorkPlace 3.5 and standard Maple, which, I am told, you already know. The examples are not important; what we want to compare is the input and output modes of the two environments.
Maple Input:
diff(sin(x+y)/cos(x-y),y);
Let us go to Maple itself and see how this works.
Maple Output:
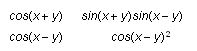
Scientific WorkPlace 3.5 Input:
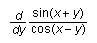
Scientific WorkPlace 3.5 Output:
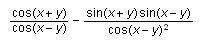
Maple Input:
diff(cos(x+y)/cos(x-y)-sin(x+y)*sin(x-y)/cos(x-y)^2,x;
Scientific WorkPlace 3.5 Input:
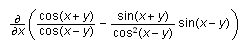
Scientific WorkPlace3.5 Output:
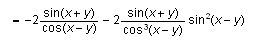
In Scientific WorkPlace 3.5, all mathematical objects, both input and output, are live:
You can copy them, paste them, change them, embed them in other objects, recalculate them, etc.
What do I mean by live mathematics?
Live Mathematics:
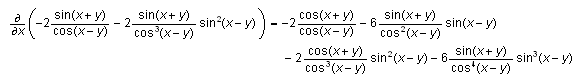
Maple Input:
M:=matrix(4,4,[1,2,0,1,2,0,3,5,3,0,-3,1,9,2,0,1]);
In Maple, the input syntax is "live," the mathematical output is not.
Maple Output:
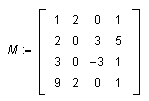
Scientific WorkPlace 3.5 Input:

Scientific WorkPlace 3.5 Output:
 You
can manipulate this matrix in a multitude of ways. Take a look at the Matrix
Menu:
You
can manipulate this matrix in a multitude of ways. Take a look at the Matrix
Menu:
The following easy steps generate the matrix

-
Click on the Math Display button.
-
Insert the
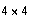 matrix template.
matrix template.
-
Enter the numbers
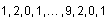 using the TAB key to advance through the empty fields.
using the TAB key to advance through the empty fields.
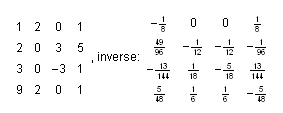
Here is how you can use Scientific WorkPlace to invert this matrix:
-
Place the cursor against the right border of the matrix.
-
Click the Compute > Matrices > Inverse buttons, in that order, and Scientific WorkPlace produces the output
Eigenvalues? They are easy to find, at least as rational approximations.
 ,
eigenvalues:
,
eigenvalues:
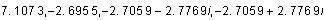
This result is produced with the following steps:
-
Place a decimal point after one of the entries of the matrix. (This tells Scientific WorkPlace that it can use an approximation algorithm to calculate the eigenvalues.)
-
Place the cursor against the right border of the matrix.
-
Click the Compute > Matrices > Eigenvalues buttons, in that order.
STANDARD BLACKBOARD
-
Students see mathematics evolve, sequentially, one example at a time.
-
Students copy from the board.
-
Teachers erase the board and start again.
-
Students go home and rewrite their notes.
"SCIENTIFIC WORKPLACE 3.5" BOARD
-
Students see mathematics evolve, in parallel, several examples at a times.
-
Students may copy from the board or wait until the end of the lecture and get a complete "play-by-play" electronic copy of the lecture.
-
Teachers can continue to work on a potentially infinite board, scroll back and forth, copy and paste, and reuse results, examples, and calculations over and over again.
-
Students and teachers can experiment to their heart's content: import new text, mathematics, and graphics.
Parallel Computations
Scientific WorkPlace 3.5 even allows you to carry out computations in parallel. This feature has amazing pedagogical potential:
Pedagogical Benefits
-
Teachers can prepare live presentations.
-
Teachers can interlace their lectures with prepared material and use short-cuts to access frequently required facts.
-
Teachers and students can access mathematical databases containing proofs, definitions, exercises and examples.
-
Teachers and students can reuse every lecture and rework and cross-reference their material with infinite variety.
THE POSSIBILITIES ARE UNLIMITED.
Personal Experience
-
TeX and LaTeX user for longer than I care to remember.
-
Scientific Word user since it was first created.
-
Scientific WorkPlace user since it was first created.
-
Maple user for four years: in the teaching of linear algebra and a special course introducing students at all levels to interactive mathematics.
Teaching and Evaluation
-
Students work in small teams of 3 or 4 students per team. At least one member of each team should be a computer enthusiast.
-
Student evaluations are a mix of marks based on team projects and individual examinations.
Pedagogical Risks
-
Lack of traditional manual drill.
-
Short-cuts may obscure mathematics.
The same arguments that were advanced against the use of pencil and paper, the slide rule, and the calculator.
These obstacles can be overcome by specifying precisely the tools allowable for the solution a problem and by requiring a reasonable amount of manual work.
To Summarize
With Scientific WorkPlace 3.5 it is now possible to teach interactive courses in linear algebra, calculus, differential equations, etc., that deal dynamically with concepts and calculations through live screen objects that can be manipulated and recomputed instantly ad infinitum.
Jim Stewart will talk to you tomorrow about precisely such a project for the teaching and learning of calculus.
The arithmetic obstacle to computationally complex problems has been eliminated.
The computational capacity of Scientific WorkPlace 3.5 makes it possible to tackle without trepidation real problems involving, for example, large matrices whose eigenvalues cannot be found algebraically. Such problems used to be relegated to special courses such as numerical linear algebra.
Among the additional features made possible by Scientific WorkPlace 3.5 are the creation of electronic databases in which all definitions, theorems, proofs, and exercises are accessible through the Scientific WorkPlace navigator.
In my forth-coming linear algebra book, for example, I have created databases for definition, theorem, and examples, as well as for proofs, and use the hyperlink capabilities of Scientific WorkPlace 3.5 to navigate between different proofs:
In an interactive session, the database files can be opened as supplementary documents, and the navigator provides direct access to the information in them. Each item can be inspected, copied, and integrated into an active session as desired. This feature provides a new electronic teaching and learning tool.
Since all mathematical data in Scientific WorkPlace 3.5 are live, they can be modified instantly on screen for further analysis and computation. No longer is there any need to erase an example before being able to present a new one or modify an old one.
As I pointed out earlier, an entire lecture can be relived by scrolling through an evolving document. This permanent record of a teaching session can be placed on a server or copied to a student's diskette and provides a live basis for home study.
Never has mathematics been so accessible.
Added 04/19/96; revised 12/08/03
This document was created with Scientific WorkPlace.