Document 108
Building An Information Superhighway Between Student and Teacher
Jonathan Lewin
Professor of Mathematics, Kennesaw State University, Marietta, Georgia
Abstract
In today's academic environment, many students are denied the sort of quality student-teacher interaction that was taken for granted when their courses were designed. As a result of this lack of communication, academic standards have suffered, particularly in disciplines such as mathematics.
This article suggests a way of opening up a line of communication between student and teacher using Scientific WorkPlace, a spectacular new scientific word processing system and front end for symbolic manipulators such as Maple and Mathematica. Our intention is to enable students to submit questions, homework and tests to their instructors and to receive assignments, handouts and lecture notes — all by e-mail or by a simple operation in a computer lab.
This article also displays some of the features of Scientific WorkPlace as a front end for Maple and Mathematica and reveals the simplicity with which mathematical operations can be performed in Scientific WorkPlace.
Table of Contents
- The Communication Dilemma
- A Software Solution of the Problem
- Scientific WorkPlace as a Word Processor
- The Scientific WorkPlace Front End for Maple and Mathematica
- In Conclusion
- Some Ordinary Differential Equations
1.0 The Communication Dilemma
The reality of today's college environment, particularly in a commuter school like the one in which I teach, is that many students maintain their own households and support themselves by working long hours at their jobs. To accommodate the needs of such students, many institutions have been compelled, in recent years, to reduce sharply the number of lectures that are given in each course and to make each lecture correspondingly longer. These longer lectures impose a grave burden on students who simply cannot stay alert for so much time. Furthermore, it is quite common for students in this kind of course to arrive on campus for their classes and then to leave as soon as soon as they can to return to their places of employment. This makes it hard for student and teacher to engage in the one-on-one dialogue that students may need in order to study mathematics successfully.
Unfortunately, the classical format of a typical college or university mathematics program is designed for the traditional full-time student who spends most of his/her time on campus and has ample access to the teacher. We need to face the fact that one of the root causes of student failure is our own failure to recognize that our classical teaching technique was designed to fit an environment that no longer exists at many schools.
The purpose of this article is to suggest a solution to this communications dilemma. I shall suggest a way of using modern technology to give our students the individual care they need even when we cannot meet them face to face. Students will be able to talk to us, to receive lecture notes, to question us, to submit assignments to us and even to be tested by us when they are not in our physical presence. In other words, I shall suggest an efficient way in which students of science and mathematics can engage in what has come to be called distance learning.
2.0 A Software Solution of the Problem
2.1 Desired Capability of The Software
For the establishment of an adequate line of communication between teacher and student, we need two basic ingredients:
- Both teacher and student need to have access to a personal computer. Ideally, these computers should be networked or, failing that, they should be connected with e-mail. If neither a network nor e-mail are available then students and their instructors can still send diskettes to each other.
- Both teacher and student should have access to special software that enables almost effortless reading and writing of complex mathematical material at the computer display and also provides effortless symbolic manipulation of such material. In addition, the documents should be stored as plain text files that can be sent back and forth easily by e-mail.
It is the second of these two ingredients that has, until now, been most elusive. None of the standard word processing products that I have seen is sufficiently versatile or easy to use to serve as a medium of communication. However, I am glad to report that this void has been filled recently by a product known as Scientific WorkPlace.
2.2 Scientific Word and Scientific WorkPlace
Scientific Word is a strikingly new kind of word processing utility that works by front ending the sophisticated LaTeX typesetting system. It is quite unlike any other word processing product on the market and there I believe that it is the word processor of choice for almost all kinds of scientific and mathematical writing. Scientific Word is also sold bundled together with Maple [Maple V is a product of Waterloo Maple Software.] V, Release 3 or with a link to Mathematica [Mathematica is a Product of Wolfram Research Inc.] and this bundle is known as Scientific WorkPlace. In Scientific WorkPlace, the word processing features of Scientific Word act as an extremely user-friendly front end for Maple or Mathematica and, in this way, Scientific WorkPlace provides the ultimately user-friendly symbolic manipulator and graphing utility.
From the perspective of working with students, it is not the ability of Scientific WorkPlace to produce professional quality output that is so important. Rather, it is the fact that Scientific WorkPlace is so easy to learn and that document preparation is so fast. It takes me only two meetings with my classes in the computer lab before the overwhelming majority of my students are comfortable with the process of using Scientific WorkPlace to read and write documents and to perform mathematical manipulations.
Part of the essence of Scientific WorkPlace is that it is so simple to use. The user does not have to be concerned about such things as tab stops, fonts, margins, hyphenation, pagination, space to be left between lines and other similar time-consuming visual activity that is, unfortunately, the bread and butter of writing with other word processing systems. Instead, Scientific WorkPlace is based on a principle known as logical design that is described in Section 3.2.
2.3 Making The Software Available
On our campus we have Scientific WorkPlace installed in faculty offices and in several computer labs to which students have access. All of these computers are hooked onto a network and all students and faculty have e-mail accounts.
In addition, some of our students and faculty have chosen to acquire their own copies of Scientific WorkPlace which they have installed on their computers at home.
2.4 Using Scientific WorkPlace to Communicate with Students
As I prepare my courses, I write up sets of lecture notes in
Scientific WorkPlace. I do so, not merely because I want these notes to be available to my
students, but because the process of writing my notes in Scientific WorkPlace is the
easiest and fastest way for me to make them. One of the logical drives seen by my office
computer is drive P: which belongs to our network. Anything I place in drive P: is visible
in read-only form to our students in the computer labs. So, for example, my students in
Mathematics 202 know that they can find material in the path
P:\files\math\lewin\202
which is constantly being updated and expanded.
One of the documents in this directory is ask202.tex. When students come to see me in my office I open this document in Scientific WorkPlace. I find it worth while to write both the question that the student is asking me and my response to the question directly into the Scientific WorkPlace document on my screen. The typing is so easy that it is actually easier for me to answer this way than to write with pencil and paper. When I am done, I save the document. From this moment on, any of my students can see that this question has been asked and they can read my response. I have found that many of my students are grateful to see the answers to questions that they themselves could not ask, either because of lack of opportunity or because they were unwilling to reveal their ignorance of the material.
Unfortunately, the academic computing department at my institution has not (yet) provided a really simple method for students to submit material to me. They cannot place their work in drive P: for me to pick up because, as I have said, the P: drive is read-only from any student operated computer. My suggestion to academic computing (which has, so far, produced nothing much more than a puzzled stare) is that they supply a new logical drive Q: that would be write-only to students. An added requirement of such a write-only drive is that a student should not be able to overwrite a file that is already placed there. This would prevent a student from accidentally erasing anther student's work.
In the meantime, I teach my students how to place their SWP
document into their e-mail and to send me an e-mail letter that looks something like the
following:
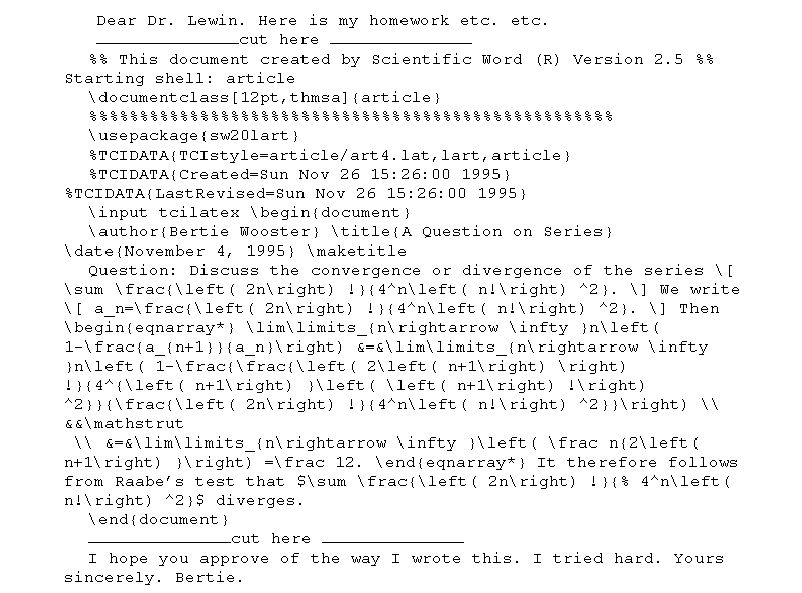
After I receive Bertie's e-mail letter, all I have to do is copy his Scientific WorkPlace document to my clipboard and then paste it into a file that I might call bwooster.tex. I can then open his document in Scientific WorkPlace, write my comments and then e-mail it back to him.
Thus, using Scientific WorkPlace, students can send and receive mathematical documents very easily even if they are restricted to a text only type of e-mail. Students who are unable to meet with the professor personally can still submit questions, homework assignments, projects and tests in the form of Scientific WorkPlace documents. By using the network or e-mail to answer many of the questions that must today be answered during their office hours, professors are able to enhance the level of contact they have with students and to make much more efficient use of their office hours. Instead of simply waiting in their offices for students who may or may not turn up, professors will be able to work at the computer screen communicating with their students. Even a student who is out of town at the time of a given lecture can receive a perfect set of lecture notes by providing his/her e-mail address. This is the sense in which Scientific WorkPlace can help us to set up an "information superhighway" between student and teacher.
2.5 Some Added Benefits
One of the most difficult lessons to convey to students of mathematics is that true learning does not take place unless the student has learned to write mathematics in such a way that the sentences are complete, meaningful and readable. All too often, college students are victims of the poor teaching (often coupled with multiple choice testing) that they experienced in their prior schooling. All too often, their work consists of a bunch of meaningless symbols that are dotted aimlessly around the page together with an "answer" that is gift wrapped in a big box.
In order for a mathematics course to be truly successful, we have to break this habit. In my opinion, the most fundamental principle of mathematics teaching is that the process of learning mathematics must be seen as being identical to the process of learning to teach mathematics. Whatever mathematics a student writes should be presented as if the student were teaching it to whomever will be reading it. In becoming a good teacher, a student is becoming a good teacher to him or her self.
I mention all this because I have noticed, among my own students, that the moment they start writing their mathematics on the computer screen they start taking pride in the appearance of their work and in the quality of their mathematical writing. As their writing improves, some of their lifelong bad habits begin to disappear and they become better problem solvers. I believe that the learning of mathematical word processing should be part and parcel of the training that students receive in a university or college mathematics curriculum.
2.6 Other Goals
The availability of Scientific WorkPlace will encourage teachers to write up their lecture notes and to make them available to their students. The advantages of compiling such lecture notes are as follows:
- Teachers who prepare polished lecture notes may give more organized and polished lectures.
- Students who are ill or out of town will still have the course materials at their fingertips.
- Students who lack note taking skills will still have a proper set of lecture notes.
- Courses may come to depend less on expensive (and often worthless) textbooks.
- Teachers will be encouraged to make their lecture notes available to other teachers in their departments. In my own department, for example, we have (in addition to the P: drive) a logical drive H: that is visible in faculty offices but not visible at machines operated by students. We can place lecture notes, examination papers and other material on this drive, even when we don't want students to see it. Eventually, a bank of material will begin to accumulate. I believe that this facility will enable the members of a department to communicate more closely with each other. It can serve as a basis for faculty discussion and it can be used to guide new faculty and part time faculty.
3.0 Scientific WorkPlace as a Word Processor
In this section I shall provide a brief discussion of the way in which I believe a mathematics course can benefit from the word processing features of Scientific WorkPlace. In the next section I shall discuss the capabilities of Scientific WorkPlace as a friendly front end for Maple or Mathematica.
3.1 Getting the Students Started
Every one of my classes begins with a couple of sessions in the computer lab where I instruct my students in the rudiments of Scientific WorkPlace. I make no attempt to teach them everything that Scientific WorkPlace can do. Instead, I teach them exactly what they need to know: how to open a document, how to preview it or print it, how to write in a document that has already been opened and how to perform mathematical operations using Maple or Mathematica.
After these initial sessions, the students can use the lab computers at any time when they are not being used by another class. I encourage those students who have their own computers to acquire the student version of Scientific WorkPlace if they can afford to do so. Many of my students have done this.
To simplify their lives even more, I have placed a document called labdoc.tex in the P: drive and instructed students to open this document and save it with another name on a diskette. If they forget to save the file onto a diskette they receive an error message because the P: drive is read-only to them. This document labdoc.tex has been set up with instructions that allow them to get going with their typing without having to make any formatting or style decisions before they begin. If they decide to print the document they have written it will be perfect. If they e-mail the Scientific WorkPlace document to me then I can open it and read it on my own machine.
If I place a homework assignment on the P: drive for my students then all they have to do is open the Scientific WorkPlace document insert their solutions directly into it. If they decide to print their work, the printed copy will be automatically hyphenated, paginated and formatted and will have the appearance of a publication quality document. Alternatively they can e-mail back the Scientific WorkPlace document for me to read on screen; in which case, I can e-mail it back with corrections and comments. Note that even complicated documents that contain binary pictures can be sent over e-mail, even if the e-mail system is primitive and allows only text files. The reason for this is that Scientific WorkPlace can store documents in a "wrapped" form in which the entire document, pictures and all, is a plain text file
At worst, if network drives and e-mail are not available, then the teacher can make the file available on diskette and the students can return the diskette with their completed homework. This is still vastly superior to handing in homework that has been written with pencil and paper.
I have found that even those of my students who are not particularly computer or keyboard literate can become comfortable with the use of Scientific WorkPlace. After a little practice with Scientific WorkPlace, they too are able to write complicated mathematical expressions effortlessly the computer screen.
3.2 Typing up a Scientific WorkPlace Document
Although it is not the primary purpose of this article to extol the virtues of Scientific WorkPlace I need to say something about the way in which the process of typing in Scientific WorkPlace differs from the process of typing in other word processing systems. This difference plays a very important role in the ability of students to write up their work quickly and effortlessly in Scientific WorkPlace.
Scientific WorkPlace operates very differently from other word processors. Unlike all of the standard word processors (such as Describe, Wordperfect, Wordpro and Microsoft Word) that are designed as "wysiwyg" (what you see is what you get) products, Scientific WorkPlace is based on an entirely different philosophy that is called logical design. [I find it interesting that the developers of Scientific WorkPlace (TCI Software Research) were also the developers, a decade ago, of the T3 scientific word processing system which was one of the very first wysiwyg word processing systems and which won an Editor's Choice award from PC Magazine in 1986 for its excellence as a technical word processor. TCI was one of the first software developers to embrace wysiwyg and now they are the first to abandon it for something better.]
The idea of logical design is that the author of a document need not also be responsible for making decisions about the way the document will look when it is printed. In other words, the author of a document should be just that: an author - not a secretary. The process of writing up a Scientific WorkPlace document is akin to the process or writing up a pile of handwritten notes that are to be handed to a secretary for typing. The secretary will shoulder the duty of producing a manuscript that is fit for publication. Since Scientific WorkPlace takes over the role of secretary, the author need not bother with such traditional nit picking issues as margins, tabs, fonts, spacing between sections, hyphenation of words, pagination of the document etc. Thus the author can focus only on what is to be written, which makes the process of preparing a document considerably simpler in Scientific WorkPlace than in other systems.
Moreover, the secretarial functions of Scientific WorkPlace go far beyond the duties of a human secretary. Scientific WorkPlace provides automatic numbering of chapters, sections, theorems, exercises, mathematical displays etc. It provides automatic cross referencing, automatic table of contents and automatic index. If changes, additions or deletions are made in a document, all of these items are updated automatically.
Even more exciting features are in the pipeline. For example, the next version of Scientific WorkPlace will allow insertion of hypertext links and will include an on-screen table of contents that will enable the user to jump to any particular section by a simple mouse click. It will also provide a history feature that will allow the user to jump back to the place of origin. Because of these features, the next version of Scientific WorkPlace will be particularly well suited for the production of documents that are meant to be read on the computer screen.
3.3 Workshops for Faculty
In order for the students to benefit properly from a knowledge of Scientific WorkPlace, it is important that as many as possible of their courses make use of it. Therefore, it is necessary to convince as many as possible of the professors in a department to take the trouble to become competent Scientific WorkPlace users. In my own department we conduct frequent workshops in order to train our faculty to become efficient users of the system.
As the system becomes accepted as the principal word processor in a given department, members of the department should start exchanging lecture notes, homework assignments, test papers and other material that has been written in Scientific WorkPlace documents. If the department computers are linked by a network then it would be a good idea to provide a special place in the network for this shared material.
4.0 The Scientific WorkPlace Front End for Maple and Mathematica
Apart from its role as a communications medium between student and instructor, Scientific WorkPlace also serves as a front end for the symbolic manipulators Maple and Mathematica, and this feature of the software gives it a second important role in the teaching of many modern mathematics courses.
In this short article, I can't even begin to describe all of the Maple and Mathematica operations that are supported by the Scientific WorkPlace. I shall demonstrate just a few of them in order to whet the appetite for more and to exhibit their intuitive simplicity. This simplicity is the key difference between symbolic manipulations in Scientific WorkPlace and symbolic manipulations in any other software product that I have seen. In order to use either Maple or Mathematica directly, or any of the other symbolic manipulators, it is necessary to type an instruction in the native language of the product. Personally, I find the process of learning these native languages to be quite painful and I find the process of remembering what I have learned to be almost as painful. Furthermore, even when the language of a symbolic manipulator has been learned, the process of writing commands in this language is slow and tedious and prone to errors. The process of working this way with my students does not appeal to me.
In sharp contrast, all of the symbolic manipulations that are performed by Maple or Mathematica in Scientific WorkPlace can be obtained by a couple of simple mouse clicks that are applied to mathematical expressions that appear on the screen in exactly the same form in which we would have written them down on paper. Anyone who knows how to write the mathematical expressions with pencil and paper automatically knows how to perform operations on the expressions with Maple or Mathematica in Scientific WorkPlace. It takes me only a few minutes to make my students feel like expert users. To display this contrast I have included with some of the following examples a brief description of my attempts to solve the same problems working directly in the front end that is supplied with Mathematica Version 2.2.3 for Windows. [Although I have ragged Mathematica a little in this section, I must emphasize that Mathematica is a first class high end symbolic manipulator. There are many important types of application for which Mathematica is a sine qua non. No doubt, my failure to produce results working directly in Mathematica is the result of my own incompetence. The point is, however, that though I am equally incompetent when I communicate with Maple or Mathematica inside of Scientific WorkPlace, I can, nevertheless, perform any operation I like that way.]
4.1 Matrix Operations
Typing a matrix is easy. In order to type the matrix

all one has to do is click on the matrix button to obtain an empty grid, select the size
and then fill it in, moving around with the mouse or the arrow keys. To type this matrix
in any of the standard symbolic manipulator front ends one has to type something like
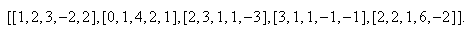
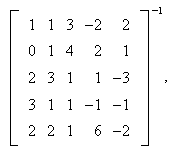
In order to invert this matrix using any of the standard manipulators one would now need
to type some inversion command that I've forgotten. However, in Scientific WorkPlace I can
ask Maple or Mathematica to invert this matrix, simply by raising it to the power of -1
yielding
opening the Maple or Mathematica menu and clicking on simplify, yielding

or clicking on evaluate numerically, yielding
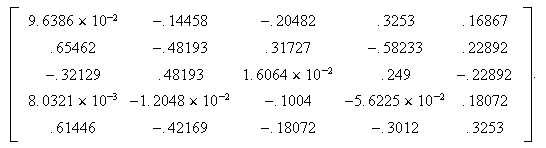
4.2 Some Simple Evaluations
To evaluate the limit
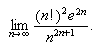
in \emph{Scientific WorkPlace},\/ one simply has to click on the Maple or Mathematica menu
and then click on the option \textsf{evaluate.} This will produce the answer:
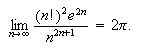
I tried several times to evaluate this limit using Mathematica directly but I never did
succeed. For my fifth try I typed
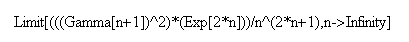
which yielded several complaints about essential singularities. Then I gave up. Presumably
there is a way to ask Mathematica to find this limit but it is beyond me and I dread the
thought of teaching it to students.
Some other expressions that I evaluated in Scientific WorkPlace
by clicking on simplify are the following:
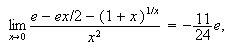
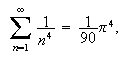
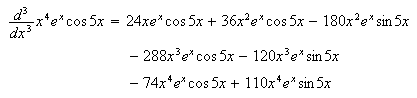
4.3 Evaluating an Integral
To evaluate a simple integral such as
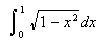
in Scientific WorkPlace, all one has to do is type the expression, place the cursor there,
click on Maple or Mathematica and evaluate. This yields
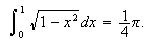
I also asked Mathematica to find this integral directly. After a couple of tries I finally
typed
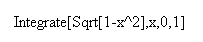
and I received output that looked something like
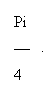
I returned to Scientific WorkPlace and typed the harder integral
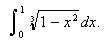
A click on Evaluate gave
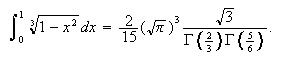
(I decided that I didn't want to see the latter expression working directly in
Mathematica.) Clicking on Evaluate Numerically yielded
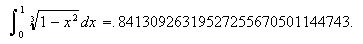
4.4 Solving an Ordinary Differential Equation
I am no expert on differential equations but I thought I should
show one anyway. So I began with the equation

When I placed the cursor in this equation clicked on the Maple option Solve ODE, I
obtained,
Exact solution is :
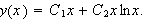
Since Equation (1) is a simple Euler equation I decided to spice it up a little. So I
tried a bunch of variations. For each of these I clicked on the Solve ODE option in
Maple. The results included Bessel functions, hypergeometric functions and various other
special functions that I have never heard of. Then, quite by accident I tried the equation

Exact solution is :
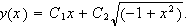
I don't know what it is about Equation (2) that distinguishes it from equations like
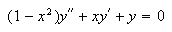
whose solutions involve special functions. But this experimentation with Scientific WorkPlace taught me something that I could never have discovered on my own. Finally, I tried some nonhomogeneous variations of Equation (2). Among these, the equation
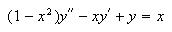
gave me
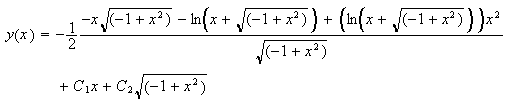
and the equation
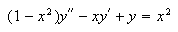
gave me
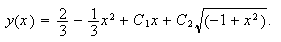
I think that the simplicity of Scientific WorkPlace makes it an ideal tool for experimentation. I would have liked to try these equations directly with Mathematica as well but I simply couldn't see how to make Mathematica recognize the symbol
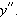 .
I got as far as
.
I got as far as 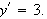 solving the equation . For this purpose I had to type
solving the equation . For this purpose I had to type 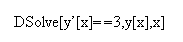
which yielded the output
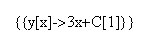
Scientific WorkPlace gives the solution as y(x)=3x+C1 which I kinda prefer.
4.5 Using the Maple or Mathematica Front End as a Writing Tool
The combination of the powerful word processing features of Scientific WorkPlace and the way it works as a front end to Maple and Mathematica allows us to write many kinds of documents very rapidly and simply; much more rapidly than one could possibly write the document with pencil and paper.
Let us suppose, for example, that we wish to test the series
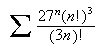
for convergence. Typically, one would begin with the words:

for each positive integer n. In order to write Equation, 3 there is
no need to retype the expression 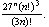 .
Since this expression appeared in the previous line, it can be reproduced
at once with a drag and drop mouse action. The next step in testing this series
is to say that for each n,
.
Since this expression appeared in the previous line, it can be reproduced
at once with a drag and drop mouse action. The next step in testing this series
is to say that for each n,
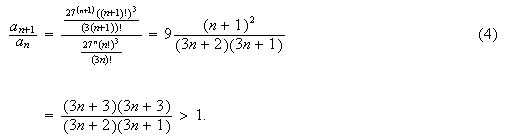
and to conclude from the fact that the sequence (an) is
increasing that  diverges.
diverges.
I shall describe now how I typed the material in the display 4: I
began by typing
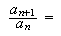
and, on the right of the = sign, I created a fraction object. Then I used
a mouse drag and drop to paste 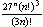 both above and below the fraction bar yielding
both above and below the fraction bar yielding
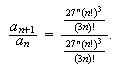
Next, I highlighted the top and used search-replace to replace

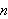 by
by

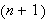 yielding
yielding
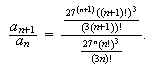
Then I typed another

 sign, and use a mouse drag and drop to produce
sign, and use a mouse drag and drop to produce
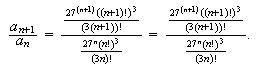
Finally I highlighted the second of the expressions
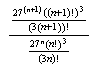
and (holding down the control button), I clicked on
simplify, yielding
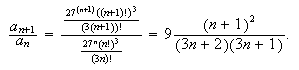
This entire process can be done in a flash.
4.6 Using the Maple Define Utility
I shall now show how to test the series
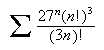
for convergence even more rapidly using the Maple define utility. As before we begin with
the definition
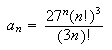
but this time we inform Maple of the definition. We highlight the above equation, open the
Maple menu and click on define, and then on New Definition. We then type
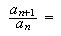
and
copy the expression

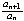 to obtain
to obtain
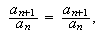
4.7 Drawing a Graph
As with other Maple operations, the drawing of graphs is simple and quick. So is the act of rotating the graphs and zooming towards them or away from them. The entire process is simple enough to encourage students to experiment with a large number of examples, to make them feel like experts and to provoke them to learn from their experience. I have included just a few of the many kinds of graph that can be drawn.
To draw the graph
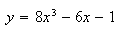
I highlighted the right side of the preceding equation, opened
the Maple menu and clicked on Plot 2D, Rectangular. This yielded
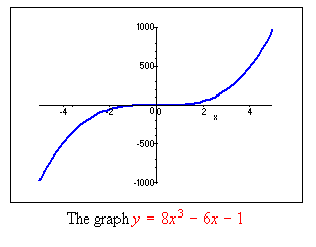
which, after a bit of zooming, came out as
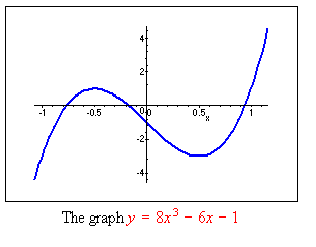
To draw the graph
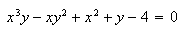
I simply selected Plot 2D Implicit from the Maple menu and obtained
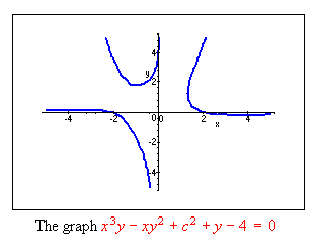
To draw the graph
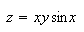
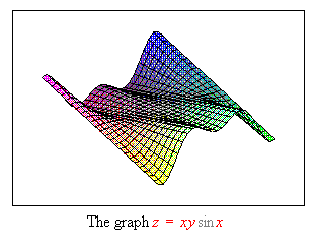
To draw this surface I highlighted the right side, opened the Maple menu and clicked on Plot 3D, Rectangular. This graph is just one of a wide variety of possible graph types that are supported by Scientific WorkPlace.
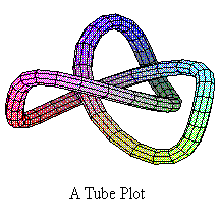
The possibilities are endless. A thickened form of the parametric
graph
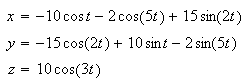
came out as
Finally, the Möbius band
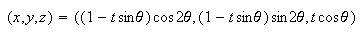
came out as

5.0 In Conclusion
The value of Scientific WorkPlace as a tool for the teaching of mathematics is twofold:
- Scientific WorkPlace's unique word processing capability makes it ideally suited as a communications medium between teacher and student.
- As a front end to Maple and Mathematica, Scientific WorkPlace provides simplicity and convenience that is not available with other products. Students using Scientific WorkPlace can be taught rapidly and simply to perform complicated symbolic operations.
I believe that if we take advantage of these unique features of Scientific WorkPlace we can take a big step forward in our quest for quality mathematics education.
6.0 Some Ordinary Differential Equations
6.1 Example
Solve the equation
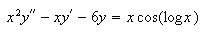

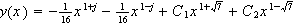
Added 06/01/96
This document was created with Scientific WorkPlace.