Document 109
Scientific WorkPlace
Roger Hunter
MacKichan Software, Inc. (formerly TCI Software Research )
Contents
Introduction
Scientific WorkPlace is a tool for the creation and use of scientific documents. By a document we mean an organized collection of information designed to communicate ideas. Under this definition, a document can exist electronically, on paper, or in any other medium. Computer algebra system worksheets, spreadsheets, Web pages, the files that underlie multimedia CD-ROMs, as well as traditional paper documents, all fall under this broad definition of document.
Scientific WorkPlace is optimized for handling mathematical content. Entering and editing mathematical expressions is simple, direct, and uses standard, natural, notation. All expressions are live---you can compute directly with mathematics in standard form.
Scientific WorkPlace complements other mathematical products like Maple, Mathematica, and Matlab. The creators of those products focus primarily on algorithms and computations. Scientific WorkPlace focuses on interface and interaction, providing simple and direct access to the capabilities of those products. At the same time, documents can be typeset with Scientific WorkPlace, producing the highest possible quality in paper form, another aspect of interaction with documents.
The emphasis on interface and interaction makes Scientific WorkPlace much more than a front end to a computer algebra system or LaTeX; it is a front end to scientific content and communication.
The use of "WorkPlace" in the name indicates how we see the product being used. It is designed as the product of choice for anyone who deals with scientific documents, including students, teachers, researchers, and professionals. By emphasizing content and logical structure, Scientific WorkPlace increases productivity, creates archival documents, and improves communication.
The Mathematics Editing Interface
Natural Notation
Natural mathematical notation is the standard notation used in printed articles, in books, and on the blackboard. Two important features of this notation are:
-
Two dimensionality. An expression like
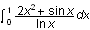 uses symbol size and positioning to convey information.
uses symbol size and positioning to convey information.
-
Single letter variable names. This makes it possible to represent multiplication with juxtaposition, increasing the information density by reducing the number of symbols needed.
Both of these features increase the speed of comprehension over the forms required by many systems. Optical bandwidth is many orders of magnitude higher than aural bandwidth, and the linear forms provide something similar to aural bandwidth. With natural notation, you can see the basic structure of very complex expressions at a glance, while it may take several minutes or more in linear form.
Developers of mathematical software systems realize the importance of natural notation, and are moving toward it for displaying expressions, although most still use linear form of notation for entering and editing.
Free-Form Editing
Scientific WorkPlace is not the only computational product to use natural notation for entering and editing expressions. Mathcad, for example, maintains expressions in what is essentially natural notation, although variable names are not assumed to be single symbols.
The unique contribution of Scientific WorkPlace is complete adherence to natural notation, together with free-form editing. The primary alternative to free-form editing is the use of complete templates. Requiring complete templates for mathematical constructs is like requiring entry of whole words when entering or editing text. Although there are only 26 characters and some punctuation in the English language, there are over 500,000 words. Similarly, there are a small number of mathematical "characters" and a large number of mathematical structures. The difference in ease-of-use provided by free-form over templates is in a similar ratio.
For example, the template for an integral is

The template is a single object with four separate fields. The only way to enter the template is to select it from a palette. Apart from the huge number of different templates necessary, this example illustrates another basic problem with templates---in natural notation, there is no clear indication of the end of the last field. The user must be aware of the boundary between the end of the last field and any following material, and must actively move out of the field. Typically, the field must be indicated on screen as a box, cluttering the screen and obscuring the notation.
In Scientific WorkPlace, the integral template is replaced by a sequence of "characters." The integral begins with the operator symbol

with two optional fields. The rest of the expression is a sequence of characters and symbols. You can insert characters at any position, and there is no need to distinguish the end of any field. The initial operator symbol with its two fields is the most complex part of the expression.
An expression consists of sequences of characters and symbols, together with what could be called character templates---fragments of expressions that represent the minimal building blocks of two-dimensional structures. The basic building blocks are shown in the following table.
| Name | Picture |
| Operator |

|
| Radical |

|
| Fraction |

|
| Script |

|
| Bracket |

|
| Matrix |

|
| Decoration |

|
| Labelled |

|
Of course, there are trade-offs. With templates, you cannot enter a malformed expression; with free-form, you can. This trade-off is analogous to the fact that you are free to misspell words in a word processor---the system does not necessarily force you to be correct. The ease-of-use in a free-form system so far outweighs the problems of entering incorrect expressions that there is simply no contest.
Computer programmers and users of traditional computational systems assume that multi-character variable names are the norm, and are surprised at a system that assumes variable names are single characters. In fact, there is a tradition in mathematics of multi-character names for special functions. The primary examples are the transcendental functions, such as sin, cos, and ln.
Rather than assume that variables are normally multi-character, and requiring that the ends of names be deduced using spaces or symbols for operations, Scientific WorkPlace assumes that all variable names are single-character, and requires you to encapsulate the characters of a multicharacter name. This process is made much easier by automatic substitution. If you type the letters s, i, and n in mathematics, Scientific WorkPlace replaces them by the single multicharacter object, sin. You can create your own multi-character names and have them recognized automatically.
Use of Color and Fonts
Scientific WorkPlace uses color to distinguish logical elements of a document. Normal text uses a black upright font while mathematics uses a red italic font. This makes the distinction between text and mathematics very clear, and at the same time allows you to insert mathematics anywhere that you can insert plain text.
Performing Computations
Basic Computations
Basic computations are performed by placing the insertion point in an
expression and choosing an operation from a menu. The results of the
computation follow the expression. For example, if you place the insertion
point anywhere in the expression
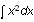 and
choose Evaluate from the Compute menu, the
result is inserted immediately following the integral sign, preceded by an
equals sign:
and
choose Evaluate from the Compute menu, the
result is inserted immediately following the integral sign, preceded by an
equals sign:
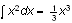 .
The insertion point is placed at the end of the result.
.
The insertion point is placed at the end of the result.
Scientific WorkPlace makes no distinction between the result of a computation and any other part of your document. There is no concept of input and output cells in Scientific WorkPlace, and performing a computation has no effect on any other part of your document. This has several advantages:
-
You can use the result directly for further computation.
-
You can edit the result in any way you want.
-
There are no special areas or cells in the document that behave differently.
-
There are no side effects that ripple through the document.
In-Place Computations
If you select any part of an expression and choose an operation from the
Compute menu while holding down the ctrl
key, the result of the computation replaces the selection. This
in-place computation provides a very powerful way to manipulate expressions.
For example, by selecting the numerator
of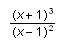
and choosing Expand, you can expand the numerator without changing the denominator:
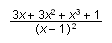
Definitions
To assign the value 27 to the variable x, you place the insertion point in the
expression
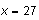 and choose New Definition from the Compute
menu. The same operation applied to the expression
and choose New Definition from the Compute
menu. The same operation applied to the expression
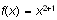 defines the function
defines the function
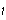 .
.
Definitions can be saved with a document and restored when it is opened.
About the Model
Scientific WorkPlace's basic computational model is directed toward easy, direct access. In this regard, it is closest to MuPAD, Maple and Mathematica. Programming capabilities provide a way of automating the basic model, and are only loosely related to document structure. Definitions are temporal---the most recent definition of a variable is in effect throughout the document, and will be used for subsequent computations until it is changed.
The other prevalent model is represented by Mathcad and Theorist, where definitions are spatial---the current value of a variable depends on where you are in a document. Programming is structural as it is in spreadsheets. In Mathcad, for example, a form of programming is achieved by linking the output of a computation in one region to the input of a computation in another.
Features of the Interface
Understanding Mathematics
Because free-form natural mathematics entry reduces the burden on the user
significantly, there is a corresponding increase in the work required by the
program to understand what the user enters. For example, the variable of
integration in an expression like
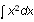 is never distinguished other than by the preceding letter d, yet we understand
the expression instantly. Our design goal was to use natural notation
exclusively, never asking the user to supply more information. These are some
of the issues that arose from this decision:
is never distinguished other than by the preceding letter d, yet we understand
the expression instantly. Our design goal was to use natural notation
exclusively, never asking the user to supply more information. These are some
of the issues that arose from this decision:
-
Many equivalent forms must be recognized---the expressions
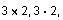 and
and
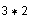 must all be equivalent.
must all be equivalent.
-
Inconsistent notation must be handled correctly---
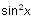 and
and
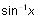 are fundamentally different in meaning yet use the same notation.
are fundamentally different in meaning yet use the same notation.
-
Natural notation is often ambiguous, with ambiguities that must be resolved differently depending on the elements of an expression. For example, the expressions
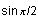 and
and
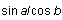 have the same form but should be interpreted as
have the same form but should be interpreted as
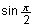 and
and
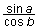 ,
respectively.
,
respectively.
These issues, and many more, are addressed during an internal translation from free-form to what amounts to mathematically complete template form. This is done every time an expression is used in a computation and it is the most complex part of Scientific Workplace's mathematics handling.
Our experience with this project bears out the statement that the more you make an interface simple and direct, the more complex it is to program. As time goes by, the percentage of computing resources devoted to interfacing will far outstrip the percentage devoted to the underlying computations. This trend is clearly evident in the rapidly increasing size of Windowing programs.
Choosing the part of an expression on which to perform a computation is
another issue that arises from the decision to make mathematics a seamless
part of a document. Scientific WorkPlace uses its knowledge of the operation
you want to perform to determine how much of an expression it chooses for the
operation. For example, suppose your insertion point is within the left-hand
side of the equation
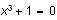 and you choose Solve Exact. Because you chose
Solve, Scientific WorkPlace selects the entire equation for
the operation, returning
and you choose Solve Exact. Because you chose
Solve, Scientific WorkPlace selects the entire equation for
the operation, returning
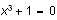 ,
Solution is:
,
Solution is:
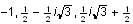
On the other hand, if you choose Factor, Scientific WorkPlace
selects just the left hand side of the expression and inserts the
factorization within the expression, yielding
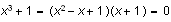
Incomplete Expressions
One of the more controversial features of Scientific WorkPlace is its ability to work with incomplete or malformed expressions. There were two motivations for this feature:
-
Deliberate shorthand should be accepted. For example,
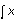 is interpreted as
is interpreted as
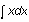 .
.
-
When the intent is obvious, minor errors should be tolerated. For example,
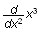 should be accepted to mean
should be accepted to mean
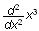 .
.
We believe this makes Scientific WorkPlace more powerful and easier to use. We're all familiar with the frustration caused by systems that insist on very rigid input syntax and add insult to injury by beeping at the slightest transgression.
The main objection to this feature is that it may encourage students to use sloppy notation. At this time, we have no evidence supporting or refuting this objection.
Another objection is that the system may interpret an expression in a way that you didn't intend. This is a consequence of the general principle that the more powerful a tool, the more potential there is for misuse.
Plots
Plotting an expression is just like performing a computation. You select the expression and choose one of the plot commands from the Compute menu. The expression is copied and stored with the plot record, so it is independent of the original expression in the document.
Plots are "live" and can be manipulated directly in place. You can use the mouse to pan or zoom a plot. To plot a second expression on an existing plot, you select the expression and drag it onto the plot.
Use for Teaching and Learning
At the time handheld calculators were first introduced, the computations they performed and the algorithms they employed were well known and available on the computers of the time. The real innovation was the method of delivery. Calculators rapidly replaced slide rules and their use led to significant changes in the actual material taught in schools.
The situation with symbolic computation is similar. At this time, the algorithms are well known and are embodied in computer algebra systems. However, classroom use is not yet widespread. There are several reasons for this, but the most important is that it takes at least the first month of each class to teach the syntax and operation of the systems before any actual mathematics can be introduced. Calculus students have to learn two languages and notations for the course instead of the one that was already a significant burden.
Because Scientific WorkPlace uses the natural notation of the textbooks and blackboard, and because it can be learned in a fraction of the time it takes to learn other systems, it can be used immediately. Like handheld calculators, Scientific WorkPlace constitutes a major new delivery system that makes the algorithms accessible to everyone.
The innovations in the Scientific WorkPlace interface make it the appropriate vehicle for the next major change in mathematics education---the widespread availability and use of symbolic computation. The impact on teaching calculus, for example, will be immense. Modern calculus classes spend most of their time on methods of differentiation and integration, exactly the mechanical aspects that are best handled by symbolic algorithms. With an accessible symbolic system available, teachers can focus on the real value of calculus---its application to solving problems. It is our conjecture that students who understand how to use the new tools to solve problems will be better at performing the mechanical computations without them.
There are many ways in which Scientific WorkPlace can be used in the teaching and learning. The system can be made available in student laboratories for exploration and assignments. It can be used in a lecture with an overhead projector. A brief outline prepared before class can be used to guide the exposition, and student "what if" questions can be answered directly by performing computations that are not obscured by interminable typing and syntax errors. The resulting document can be distributed to students, obviating the need for them to take notes.
Scientific WorkPlace is particularly suited to the trend toward getting mathematics students to write. Its word-processor format makes it easy to prepare and edit assignments, and the high-quality typeset output encourages students to take more care with their writing.
Added 01/01/96; revised 12/09/03
This document was created with Scientific WorkPlace.